ニュース
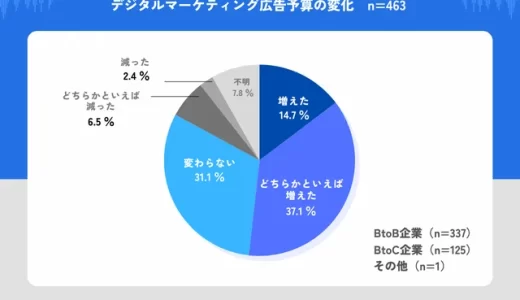
サードパーティCookie廃止後に約5割の企業の広告予算が増加 対策をしていない企業は3割以上【ナイル調査】
WACUL、マーケティングDXツール「AIアナリスト」におけるGA4との連携件数2,000件突破を発表

レブコム、オンライン会議解析AI「MiiTel Meetings」に新機能をリリース Google Calendarと連携可能に

Braze、「Sage AI by Braze」のラインアップを拡充 新AI機能がマーケティングの創造性と効率性を向上

ゼロワングロース、旭化成エレクトロニクスのマーケティングオペレーションモデル設計構築を支援

Pathee、「STORECAST」に「AIアシスト(ベータ版)」をリリース 店舗の販促活動をAIがサポート
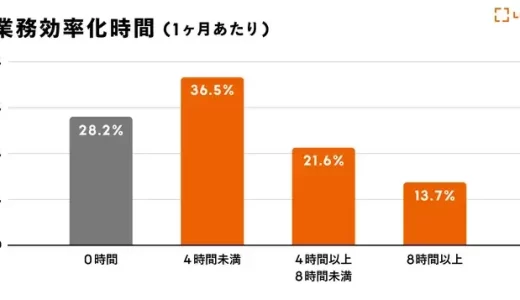
LIFULL社員の7割以上が生成AI活用による業務効率化に成功 5割以上が業務の質向上を実感【LIFULL調査】

BtoBベンチャー企業の12.9%が新年度マーケティング予算を増額 うち60%がSNSに注力予定【IDEATECH調査】

OMO施策を実施している企業は54.4% 内容は実店舗とECサイトの在庫連携が最多【東通メディア調査】
事例・インタビュー

ロイヤル顧客が「ブランドを強くする」 しゃぶ葉&Asobicaに聞く、クローズドコミュニティーを活用したファンマーケティング手法

PIMを活用した一元管理で顧客&自社課題を解決 顧客価値起点のマーケティング改革における、グローバルPIMの役割とは

ChatGPTによる「リライト」で工数減&記事順位アップ jinjerの実践するAI活用法とその成功ポイントとは

マーケティングから始める経営変革 パナソニック コネクトが取り組む「顧客価値起点マーケティング」とは

目指すは「アジアNo.1」シリーズBで35億円を調達したMicoworksが語る、成長力の秘訣と今後の展望

「正しいことを大量に実行する」ことが重要 「SEOおたく」が率いるLANYに聞く、コンテンツマーケティングの成功のカギ

登録者40万人&再生回数1億回突破 dipチャンネル運用の成功に学ぶ、Z世代に「刺さる」SNSマーケティング戦略

「U23マーケティング部」から見る地域創生 モンテディオ山形が得た成果と、チーム内外に波及する「無形の力」とは

日系大企業に新しい視点を送り込んだ外資系マーケターのキャリア形成とは【CMO Japan Summit 2023 – 小林製薬株式会社 講演】

25年目に得たブランドパーパスへの気づきとブランド確立のための戦略とは【CMO Japan Summit 2023 – ダイキン工業株式会社 講演】
解説・コラム

SEO対策会社おすすめ比較10社!SEO専門業者の選び方や注意点

上場している大手SEO会社おすすめ10社!依頼するメリットやデメリット・注意点を解説

【プロが厳選】法人向けSEO研修・講座サービスおすすめ5社比較一覧

SEO対策を外注するメリット・デメリットや費用、業者に騙されない方法

インハウスSEOとは?SEO内製化方法や外注化の違い、メリット解説

SEO内製化(インハウスSEO)支援サービス会社おすすめ6社比較

被リンク獲得代行サービスのおすすめ企業9社!信頼できる会社をプロが厳選

【2024年】GA4設定代行おすすめ企業9社!GA4支援内容や費用相場も解説

SEOコンサルタントとは?仕事内容や将来性、資格、年収を解説

SEO対策とは?基本や施策の種類、メリット・デメリットをわかりやすく解説
資料ダウンロード

【サービス資料】資料掲載・リード獲得し放題サービス「MARKETIMES SLIDE」

【資料DL】完全保存版!マーケティングに活用できるフレームワーク12選ガイドブック

【資料DL】ペルソナ設計テンプレート付き:ペルソナとは?具体的な設計方法を解説

【資料DL】SNS徹底比較ガイドブック!SNSの運用・広告の特徴を解説

【資料DL】Google Anlaytics 4(GA4)基礎・導入設定資料(全42ページ)
リサーチ

Z世代の3割がTikTok投稿を「出演者が苦手」で途中スワイプ PR施策のヒントを公開【サムライト調査】

サードパーティCookie廃止後に約5割の企業の広告予算が増加 対策をしていない企業は3割以上【ナイル調査】

LIFULL社員の7割以上が生成AI活用による業務効率化に成功 5割以上が業務の質向上を実感【LIFULL調査】

BtoBベンチャー企業の12.9%が新年度マーケティング予算を増額 うち60%がSNSに注力予定【IDEATECH調査】

OMO施策を実施している企業は54.4% 内容は実店舗とECサイトの在庫連携が最多【東通メディア調査】
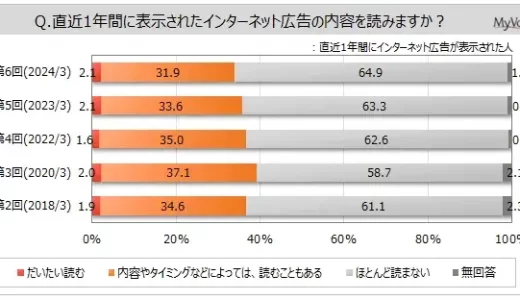
表示されたインターネット広告の種類はバナー広告が最多 広告の内容を読む人は34%【マイボイスコム調査】
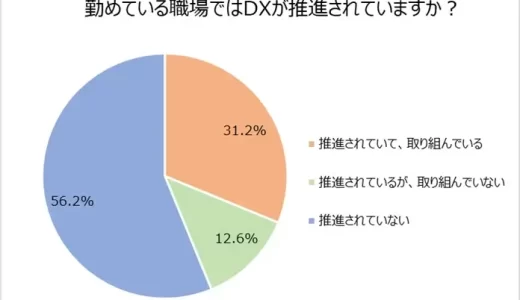
勤め先がデジタル化推進に取り組んでいる人は約3割 進まない理由1位は「経営上位層の認識の遅れ」【TOA調査】

「就活生のDX能力」を評価する大企業の採用担当者は9割超【中小企業個人情報セキュリティー推進協会調査】
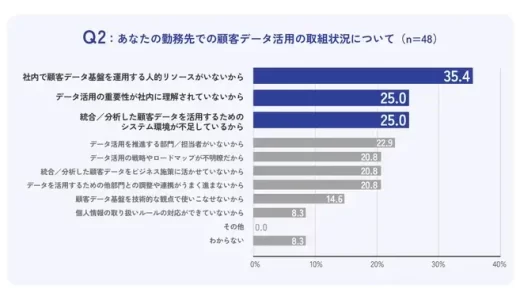
顧客データ基盤を構築運用している企業は36% しない理由1位は「人的リソース不足」【インキュデータ調査】
寶結、仮想待合室システム「Match AI」の実証結果を発表 ユーザの離脱を防ぎ予約数が250%向上
製品・サービス

WACUL、マーケティングDXツール「AIアナリスト」におけるGA4との連携件数2,000件突破を発表

レブコム、オンライン会議解析AI「MiiTel Meetings」に新機能をリリース Google Calendarと連携可能に

Braze、「Sage AI by Braze」のラインアップを拡充 新AI機能がマーケティングの創造性と効率性を向上

Pathee、「STORECAST」に「AIアシスト(ベータ版)」をリリース 店舗の販促活動をAIがサポート

ナレッジセンス、法人向けAIチャットボットシステム「ChatPro」をアップデート PowerPointの読込に対応
ソフトブレーン、CRM/SFA「eセールスマネージャーRemix」にてMA機能「esm marketing」を提供開始

wevnal、「BOTCHAN Relation」をリリース 新規購入ユーザーをLINEへ誘導しLTVを向上

フロッグウェル、SalesforceからSMS送信機能を提供開始 月額無料で顧客コミュニケーションを強化
NTTビジネスソリューションズ、対話型AIツール「karafuru AI(仮称)」提供へ AIが考え方をアドバイス

ウィルゲート、「プロトル」をリリース マーケティング・セールス領域のプロ人材と企業をマッチング
寄稿記事

SNS委員会を作っても運用できない……その2つの理由とは?

「Threads(スレッズ)」などの新たなSNSは使うべき? 注意点や運用のコツを紹介

マーケティングへのメタバース活用の可能性と成果を上げるポイント

インバウンド対策に!海外のWhatsAppマーケティング事情
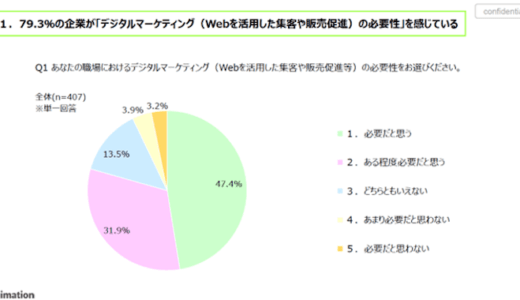
【特典付】ハマった時こそ抑えておきたい デジタルマーケティングで成果が出ない「顧客理解」という根本原因

企業X(旧Twitter)アカウント、「中の人」は立てるべき?

SNSマーケティングを始める4つのメリット

Web上の CX (顧客体験) 改善に役立つフィードバックを取得するヒント

YouTubeチャンネルの検索対策とは?重要性と方法を解説

